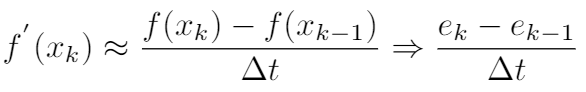PD Control

With the addition of integral gain, you were able to minimize SSE; however, you may have noticed that this came at the expense of settling time and percent overshoot. The derivative term attempts to “predict” what the error will be by linearly extrapolating the change in error value, i.e. it looks to future values (recall that the finite difference approximation of the derivative is the slope of the tangent line). By taking into account the rate of change in the error, the system can more gracefully and rapidly approach the setpoint.

Once again, however, you need to consider how to approximate a continuous-time derivative in a discrete-time system. The derivative of a function represents the slope of the tangent line evaluated at a particular point. It is possible then to approximate the slope with a single-step backwards difference formula,